Raised Equator Problem
Raised Equator Problem
This is a minor variation of a well known math problem involving the circumference and radius of a circle, and the Earth. The equator is an imaginary belt surrounding the Earth. Imagine that we wanted to raise it uniformly so that it is 1 meter above the ground. How much length should be added to the belt? Assume Earth's radius is 6,378 km (kilometers) or 6,378,000 m (meters).
Method 1: the hard way.
where C is the circumference, and r is the radius of a circle.
Current circumference C1:
Required circumference C2 adds 1m to r:
Length to add to C1 is:
where C2-C1 is the length to be added to the belt.
Method 2: easier.
where C1 and C2 are the same as above,
r1 is the current radius,
r2 is the desired radius,
r2 - r1 is the change in radius, or 1 meter.
Equation [6] shows that the change in circumference because of a change in radius is independent of the size of the circle.
Method 3: even easier but requires some differential calculus.
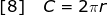



r1 is the current radius,
r2 is the desired radius,
r2 - r1 is the change in radius, or 1 meter.
Equation [6] shows that the change in circumference because of a change in radius is independent of the size of the circle.
Method 3: even easier but requires some differential calculus.
where dC is the change in the circumference, and dr is the change in the radius.
As in equation [6], equation [10] shows that the change in circumference (dC) depends only on the change in the radius (dr), not on the size of the radius or the size of the circumference. Thus, adding 1 meter to the radius requires adding 2 pi meters to the circumference regardless if it is around a grape, around the Earth, or around the observable universe.
Original Version
In the original version of this problem, 1 meter is added to the circumference. How does this affect the radius? By using method 3 and solving equation [10] for dr gives:

The change in radius is dependent only on the change in circumference and is independent of the size of the circle.
[QED]
John L. Ferri
jlferri@epix.net
As in equation [6], equation [10] shows that the change in circumference (dC) depends only on the change in the radius (dr), not on the size of the radius or the size of the circumference. Thus, adding 1 meter to the radius requires adding 2 pi meters to the circumference regardless if it is around a grape, around the Earth, or around the observable universe.
Original Version
In the original version of this problem, 1 meter is added to the circumference. How does this affect the radius? By using method 3 and solving equation [10] for dr gives:
The change in radius is dependent only on the change in circumference and is independent of the size of the circle.
[QED]
John L. Ferri
jlferri@epix.net

Comments
Post a Comment